Chapter 20 Paired-sample t-test
In the previous chapter we learnt about how blocking is a useful technique for dealing with confounding effects. However, we didn’t think about how we would analyse such data. If we’ve used a block design we can’t just throw our data into something like a t-test or ANOVA. Remember, one of the assumptions of these tests is independence of the experimental units, and yet, using a blocked design creates a situation where some units are not independent. In this chapter and the next we’ll consider versions of the t-test and ANOVA that can be used to analyse such non-independent data.
20.1 When do we use a paired-sample t-test?
There are situations in which data may naturally form pairs of non-independent observations: the first value in a sample A is linked to the first value in sample B, the second value in sample A is linked with the second value in sample B, and so on. This is known as a paired-sample data. A common example of paired-sample data is the situation where we have a group of organisms, and we record some measurement from each organism before and after an experimental treatment. For example, if we were studying heart rate in relation to position (sitting vs. standing) we might measure the heart rate of a number of people in both positions. In this case the heart rate of a particular person when sitting is paired with the heart rate of the same person when standing.
An experimental design that sets out to produce paired-data is known as a paired-sample design. More often than not paired-sample data arise as consequence of such deliberate decisions. Why? In biology, we often have the problem that there is a great deal of variation between the units we’re studying (individual organisms, tissue samples, etc). There may be so much among-unit variation that the effect of any difference among the situations we’re really interested in is obscured. Using a paired-sample design gives us a way to control for the among-unit variation and increase the power of our statistical tests. However, we should not use a two-sample t-test when our data have this kind of structure. Let’s find out why.
20.2 Why do we use a paired-sample design?
Consider the following. A drug company wishes to test two drugs for their effectiveness in treating a rare illness in which glycolipids are poorly metabolised. An effective drug is one that lowers glycolipid concentrations in patients. The company is only able to find 8 patients willing to cooperate in the early trials of the two drugs. What’s more, the 8 patients vary in their age, sex, body weight, severity of symptoms and other health problems.
One way to conduct an experiment that evaluates the effect of the new drug is to randomly assign the 8 patients to one or other drug and monitor their performance. However, this kind of design is very unlikely to detect a statistically significant differences between the treatments. This is because it provides very little replication, yet can we expect considerable variability from one person to another in the levels of glycolipid before any treatment is applied. This variability would to lead to a large standard error in the difference between means.
A solution to this problems is to treat each patient with both drugs in turn and record the glycolipid concentrations in the blood, for each patient, after a period taking each drug. One arrangement would be for four patients to start with drug A and four with drug B, and then after a suitable break from the treatments, they could be swapped over onto the other drug. This would give us eight replicate observations on the effectiveness of each drug and we can determine, for each patient, which drug is more effective.16
The experimental design, and one hypothetical outcome, is represented in the diagram below…
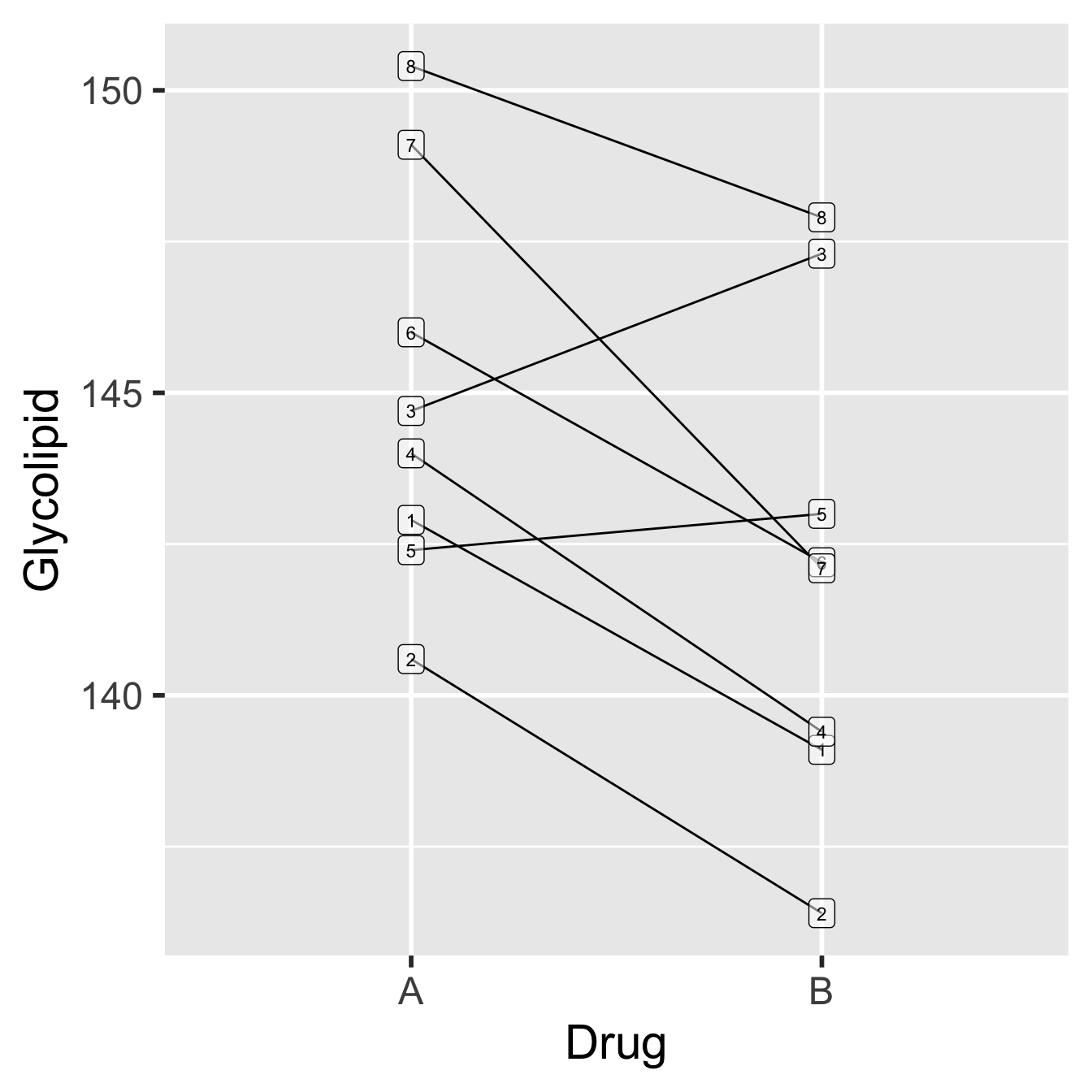
Figure 20.1: Data from glycolipid study, showing paired design. Each patient is denoted by a unique number.
Each patient is represented by a unique number (1-8). The order of the drugs in the plot does not matter—it doesn’t mean that Drug A was tested before Drug B just because Drug A appears first. Notice that there is a lot of variability in these data, both in the glycolipid levels of each patient, and in the amount by which the drugs differ in their effects (e.g. the drugs have roughly equal effects for patient 5, while drug B appears to be more effective for patient 2). What can also be inferred from this pattern is that although the glycolipid levels vary a good deal between patients, Drug B seems to reduce glycolipid levels more than Drug A.
The advantage to using a paired-sample design in this case is clear if we look at the results we might have obtained on the same patients, but where they have been divided into two groups of four, giving one group Drug A and one group Drug B:

Figure 20.2: Data from glycolipid study, ignoring paired design.
The patients and their glycolipid levels are identical to those in the previous diagram, but only patients 2, 3, 4 and 8 (selected at random) were given Drug A, while only patients 1, 5, 6, and 7 were given Drug B. The means of the two groups are different, with Drug B performing better, but the associated standard error would also be large relative to this difference. A two-sample t-test would certainly fail to identify a significant difference between the two drugs.
So, it would be quite possible to end up with two groups where there was no clear difference in the mean glycolipid levels between the two drug treatments even though Drug B seems to be more effective in the majority of patients. What the pairing is doing is allowing us to factor out (i.e. remove) the variation among individuals, and concentrate on the differences between the two treatments. This works by focussing on the differences occurring within individuals. The result is a much more sensitive evaluation of the effect we’re interested in.
The next question is, how do we go about analysing paired data in a way that properly accounts for the structure in the data?
20.3 How do you carry out a t-test on paired-samples?
It should be clear why a paired-sample design might be useful, but how do we actually construct the right test? The ‘trick’ is to work directly with the differences between pairs of values. In the case of the glycolipid levels illustrated in the first diagram, we noted that there was a greater decrease of glycolipids in 75% of patients using Drug B compared with Drug A.
If we calculate the actual differences (i.e. subtracted the value for Drug A from the value for Drug B) for each patient we might see something like: -3.9, -4.1, 2.5, -4.7, 0.5, -3.7, -6.9, -2.4. Notice that there are only two positive values in this sample of differences, one of which is fairly close to 0. The mean difference is -2.8, i.e. on average, glycolipid levels are lower with Drug B. Another way of stating this observation is that within subjects (patients), the mean difference between drug B and drug A is negative. A paired-sample design focusses on the within-subject (or more generally, within-item) change.
If, on the other hand, the two drugs had had similar effects then what would we expect to see? We would expect no consistent difference in glycolipid levels between the Drug A and Drug B treatments. Glycolipid levels are unlikely to remain exactly the same over time, but there shouldn’t be any pattern to these changes with respect to the drug treatment: some patients will show increases, some decreases, and some no change at all. The mean of the differences in this case should be somewhere around zero (though sampling variation will ensure it isn’t exactly equal to zero).
So, to carry out a t-test on paired-sample data we have to: 1) find the mean of the difference of all the pairs and 2) evaluate whether this is significantly different from zero. We already know how to do this! This is just an application of the one-sample t-test, where the expected value (i.e. the null hypothesis) is 0. The thing to realise here, is that although we started out with two sets of values, what matters is the sample of differences between pairs and the population we’re interested in a ‘population of differences.’
When used to analyse paired data in this way, the test is referred to as a paired-sample t-test. This is not wrong, but it important to remember that a paired-sample t-test is just a one-sample t-test applied to the sample of differences between pairs of associated observations. A paired-sample t-test isn’t really a new kind of test. Instead, it is a one-sample t-test applied to a new kind of situation.
20.3.1 Assumptions of the paired-sample t-test
The assumptions of a paired-sample t-test are no different from the one-sample t-test. After all, they boil down to the same test! We just have to be aware of the target sample. The key point to keep in mind is that it is the sample of differences that is important, not the original data. There is no requirement for the original data to be drawn from a normal distribution because the normality assumption applies to the differences. This is very useful, because even where the original data seem to be drawn from a non-normal distribution, the differences between pairs can often be acceptably normal. The differences do need to be measured on an interval or ratio scale, but this is guaranteed if the original data are on one of these scales.
20.4 Carrying out a paired-sample t-test in R
R offers the option of a paired-sample t-test to save us the effort of calculating differences. It calculates the differences between pairs for us and then carries out a one-sample test on those differences. We’ll look at how to do it the ‘old fashioned’ way first—calculating the differences ourselves and running a one-sample test—before using the short-cut method provided by R.
You should work through the example in this section.
Staying with the problem of trials of two drugs for controlling glycolipid levels, the serum glycolipid concentration data from the trial illustrated above are stored in the GLYCOLIPID.CSV file. Download the this file from MOLE and place it in the working directory. Read GLYCOLIPID.CSV into an R data frame, giving it the name glycolipid.
As always, we should start by looking at the raw data:
glimpse(glycolipid)## Rows: 16
## Columns: 4
## $ Patient <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8
## $ Sex <chr> "Male", "Female", "Male", "Female", "Female", "Male", "Fem…
## $ Drug <chr> "A", "A", "A", "A", "A", "A", "A", "A", "B", "B", "B", "B"…
## $ Glycolipid <dbl> 142.9, 140.6, 144.7, 144.0, 142.4, 146.0, 149.1, 150.4, 13…There are four variables in this data set: Patient indexes the patient identity, Sex is the sex of the patient (we don’t need this), Drug denotes the drug treatment, and Glycolipid is the glycolipid level.
Next, we need to calculate the differences between each pair. We can do this with the dplyr functions group_by and summarise:
glycolipid_diffs <-
glycolipid %>%
group_by(Patient) %>%
summarise(Difference = diff(Glycolipid))What we did was group the data by the values of Patient, and then used a function called diff to calculate the difference between the two Glycolipid concentrations within each patient. We stored the result of this calculation in a new data frame called glycolipid_diffs. This is the data we’ll use to carry out the paired-sample t-test:
glycolipid_diffs## # A tibble: 8 x 2
## Patient Difference
## <dbl> <dbl>
## 1 1 -3.8
## 2 2 -4.20
## 3 3 2.6
## 4 4 -4.60
## 5 5 0.600
## 6 6 -3.8
## 7 7 -7
## 8 8 -2.5We should try to check that the differences could plausibly have been drawn from a normal distribution, though normality is quite hard to assess with only 8 observations:
ggplot(glycolipid_diffs, aes(x = Difference)) +
geom_dotplot() + theme_grey(base_size = 22)## `stat_bindot()` using `bins = 30`. Pick better value with `binwidth`.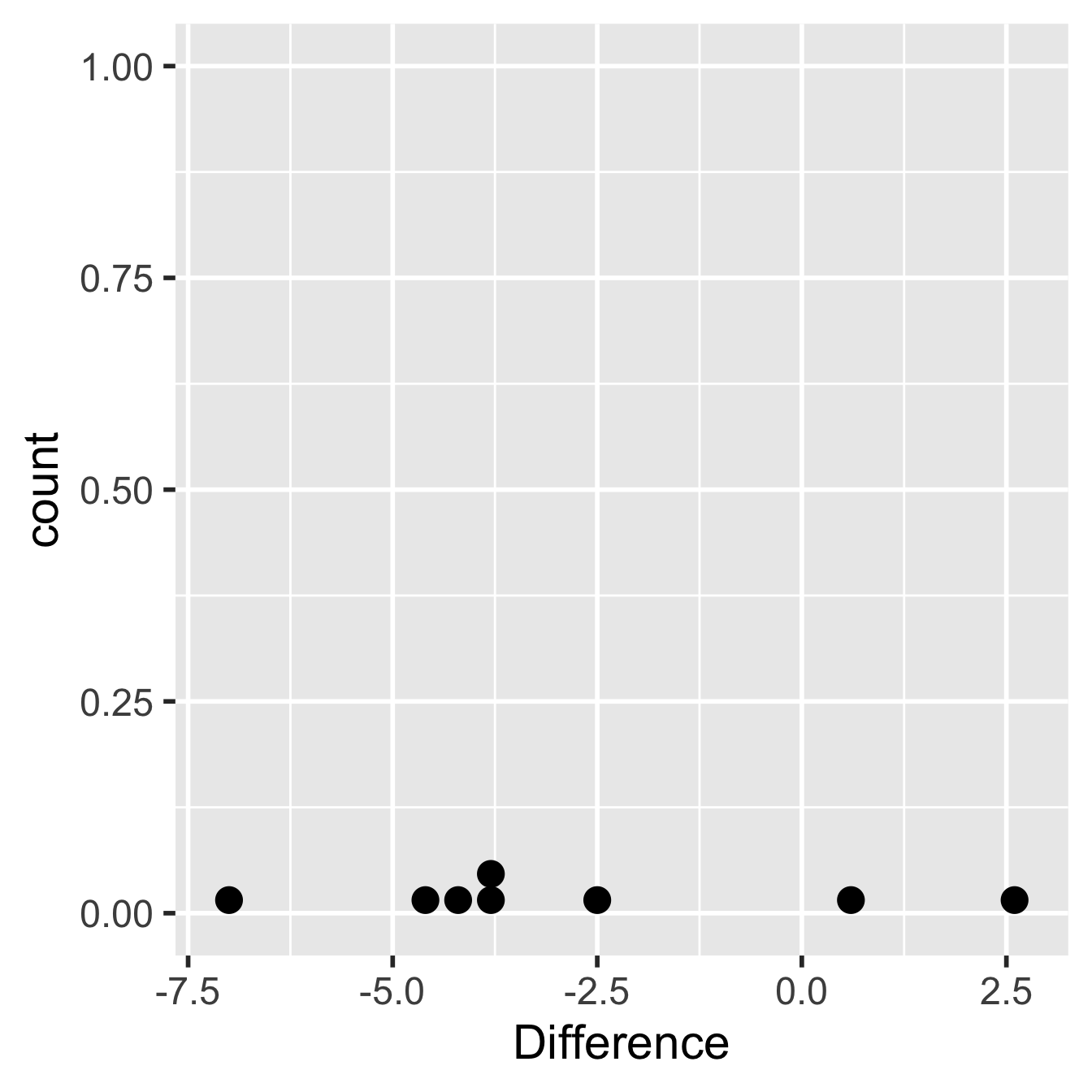
Figure 20.3: Within-individual differences from glycolipid study
OK, there really isn’t a lot of data to work with here but there’s nothing in that plot that screams ‘non-normal,’ which means the assumptions have been met as best they can be. Let’s proceed to carry out a one-sample t-test on the calculated differences. This is easy to do in R:
t.test(glycolipid_diffs$Difference)##
## One Sample t-test
##
## data: glycolipid_diffs$Difference
## t = -2.6209, df = 7, p-value = 0.03436
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## -5.397549 -0.277451
## sample estimates:
## mean of x
## -2.8375We don’t have to set the data argument to carry out a one-sample t-test on the differences. We just passed along the numeric vector of differences extracted from glycolipid_diffs (using the $ operator). What happened to the mu argument used to set up the null hypothesis? Remember, the null hypothesis is that the population mean is zero. R assumes that this is 0 if we don’t supply it, so no need to set it here.
The output is quite familiar… The first line reminds us what kind of test we did, and the second line reminds us what data we used to carry out the test. The third line is the important one: t = -2.6209, df = 7, *p*-value = 0.03436. This gives the t-statistic, the degrees of freedom, and the all-important p-value associated with the test. The p-value tells us that the mean within-individual difference is significant at the p < 0.05 level.
We need to express these results in a clear sentence incorporating the relevant statistical information:
Individual patients had significantly lower serum glycolipid concentrations when treated with Drug B than when treated with Drug A (t = 2.62, d.f. = 7, p < 0.05).
There are a couple of things to point out in interpreting the result of such a test:
The sample of differences was used in the test, not the sample of paired observations. This means the degrees of freedom for a paired-sample t test are one less than the number of differences (= number of pairs); not one, or two, less than the total number of observations.
Since we have used a paired-sample design our conclusion stresses the fact that the use of the Drug B results in a lower glycolipid level in individual patients; it doesn’t say that the use of Drug B resulted in lower glycolipid concentrations for everyone given Drug B than for anyone given Drug A.
20.4.1 Using the paired = TRUE argument
R does have a built in procedure for doing paired-sample t-tests. Now that we’ve done it the hard way, let’s try carrying out the test using the built in procedure. This looks very similar to a two-sample t-test, except that we have to set the paired argument of the t.test function to TRUE:
t.test(Glycolipid ~ Drug, data = glycolipid, paired = TRUE)##
## Paired t-test
##
## data: Glycolipid by Drug
## t = 2.6209, df = 7, p-value = 0.03436
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.277451 5.397549
## sample estimates:
## mean of the differences
## 2.8375R takes care of the differencing for us, so now we can work with the original glycolipid data rather than the glycolipid_diffs data frame constructed above. We won’t step through the output because it should make sense by this point.
Order matters
Be careful when using the built in procedure for doing paired-sample t-tests. The only information R uses to associate pairs of observations is their order in each group. The first observation in the ‘A’ group is paired with the first observation in the ‘B’ group, the second observation in the ‘A’ group is paired with the second observation in the ‘B’ group, and so on. If the items/individuals aren’t ordered the same way in each group, the test will be wrong and we’ll end up with a meaningless p-value!
R makes it easy to do paired-sample t-test. It really doesn’t matter which method we use to carry out the test. Just don’t forget that a paired-sample t-test is only a one-sample test on paired differences.
This kind of experimental design is called a cross-over study. It can be problematic if, for example, “carry-over” effects occur, e.g., the effect of one drug is altered when the other drug has previously been administered. We won’t worry about these problems here though.↩︎